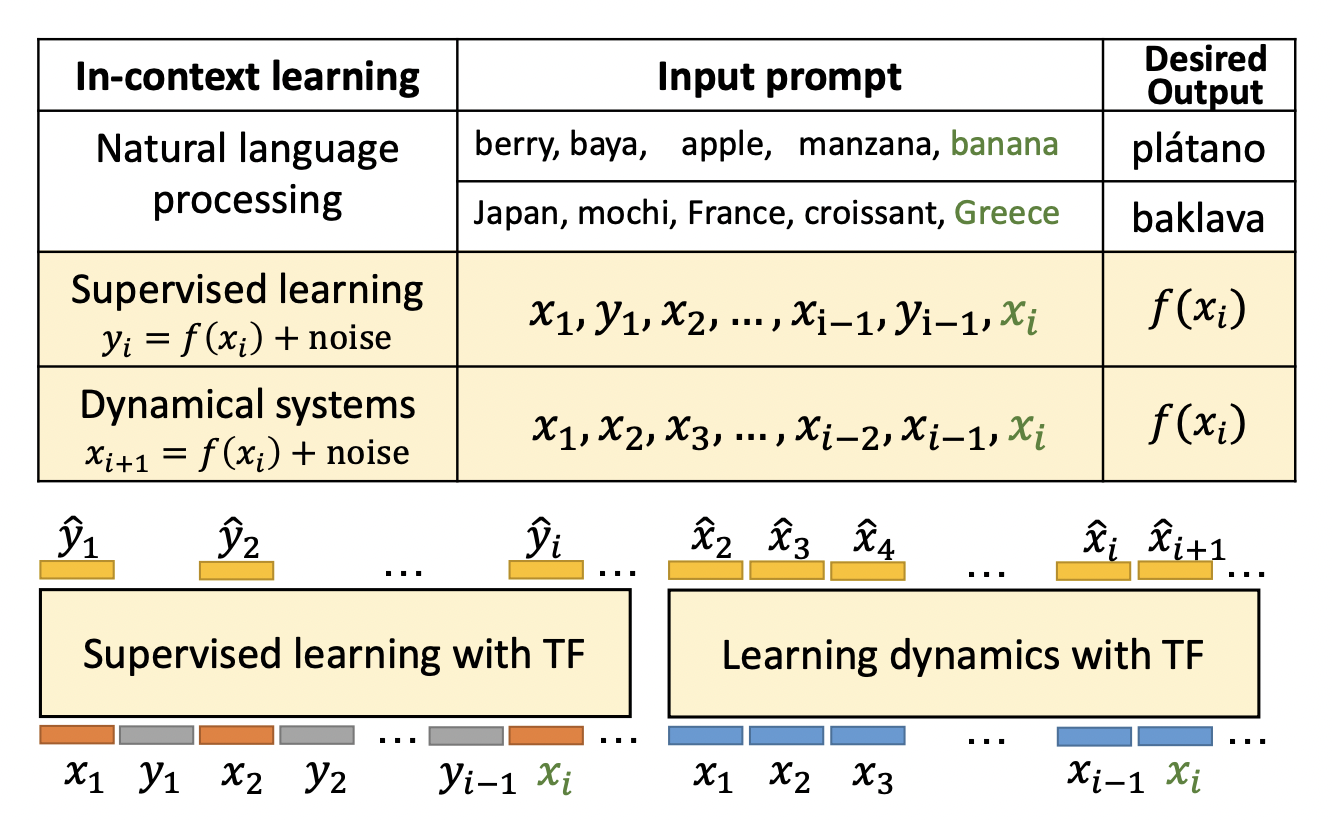
In-context learning is a recent paradigm where a large language model (LLM) observes a test instance and a few training examples as its input and directly decodes the output without any update to its parameters. This implicit training contrasts with the usual training where the weights are changed based on the examples.
Here comes the question of why In-context learning would be beneficial. You can suppose that you have two regression tasks that you want to model, but the only limitation is you can only use one model to fit both tasks. Here In-context learning comes in handy as it can learn the regression algorithms per task, which means the model will use separate fitted regressions for different sets of inputs.
In the paper “Transformers as Algorithms: Generalization and Implicit Model Selection in In-context Learning,” they have formalized the problem of In-context learning as an algorithm learning problem. They have used a transformer as a learning algorithm that can be specialized by training to implement another target algorithm at inference time. In this paper, they have explored the statistical aspects of In-context learning through transformers and did numerical evaluations to verify the theoretical predictions.
In this work, they have investigated two scenarios, in first the prompts are formed of a sequence of i.i.d (input, label) pairs, while in the other the sequence is a trajectory of a dynamic system (the next state depends on the previous state: xm+1 = f(xm) + noise).
Now the question comes, how we train such a model?
In the training phase of ICL, T tasks are associated with a data distribution {Dt}t=1T. They independently sample training sequences St from its corresponding distribution for each task. Then they pass a subsequence of St and a value x from sequence St to make a prediction on x. Here is like the meta-learning framework. After prediction, we minimize the loss. The intuition behind ICL training can be interpreted as searching for the optimal algorithm to fit the task at hand.
Next, to obtain generalization bounds on ICL, they borrowed some stability conditions from algorithm stability literature. In ICL, a training example in the prompt influences the future decisions of the algorithms from that point. So to deal with these input perturbations, they needed to impose some conditions on the input. You can read [paper] for more details. Figure 7 shows the results of experiments performed to assess the stability of the learning algorithm (Transformer here).
RMTL is the risk (~error) in multi-task learning. One of the insights from the derived bound is that the generalization error of ICL can be eliminated by increasing the sample size n or the number of sequences M per task. The same results can also extend to Stable dynamic systems.

Now let’s see the verification of these bounds using numerical evaluations.
GPT-2 architecture containing 12 layers, 8 attention heads, and 256-dimensional embedding is used for all experiments. The experiments are performed on regression and linear dynamics.
- Linear Regression: In both figures (2(a) and 2(b)), in-context learning results (Red) outperform the least squares results (Green) and are perfectly aligned with optimal ridge/weighted solution (Black dotted). This, in turn, provides evidence for transformers’ automated model selection ability by learning task priors.
- Partially observed dynamic systems: In Figures (2(c) and 6), Results show that In-context learning outperforms Least square results of almost all orders H=1,2,3,4 (where H is the window size of that slides over the input state sequence to generate input to the model kind of similar to subsequence length)
In conclusion, they successfully showed that the experimental results align with the theoretical predictions. And for the future direction of works, several interesting questions would be worth exploring.
(1) The proposed bounds are for MTL risk. How can the bounds on individual tasks be controlled?
(2) Can the same results from fully-observed dynamic systems be extended to more general dynamical systems like reinforcement learning?
(3) From the observation, it was concluded that transfer risk depends only on MTL tasks and their complexity and is independent of the model complexity, so it would be interesting to characterize this inductive bias and what kind of algorithm is being learned by the transformer.
Check out the Paper. All Credit For This Research Goes To the Researchers on This Project. Also, don’t forget to join our Reddit Page, Discord Channel, and Email Newsletter, where we share the latest AI research news, cool AI projects, and more.
![]()
Vineet Kumar is a consulting intern at MarktechPost. He is currently pursuing his BS from the Indian Institute of Technology(IIT), Kanpur. He is a Machine Learning enthusiast. He is passionate about research and the latest advancements in Deep Learning, Computer Vision, and related fields.