Input space mode connectivity in deep neural networks builds upon research on excessive input invariance, blind spots, and connectivity between inputs yielding similar outputs. The phenomenon exists generally, even in untrained networks, as evidenced by empirical and theoretical findings. This research expands the scope of input space connectivity beyond out-of-distribution samples, considering all possible inputs. The study adapts methods from parameter space mode connectivity to explore input space, providing insights into neural network behavior.
The research draws on prior work identifying high-dimensional convex hulls of low loss between multiple loss minimizers, which is crucial for analyzing training dynamics and mode connectivity. Feature visualization techniques, optimizing inputs for adversarial attacks further contribute to understanding input space manipulation. By synthesizing these diverse areas of study, the research presents a comprehensive view of input space mode connectivity, emphasizing its implications for adversarial detection and model interpretability while highlighting the intrinsic properties of high-dimensional geometry in neural networks.
The concept of mode connectivity in neural networks extends from parameter space to input space, revealing low-loss paths between inputs yielding similar predictions. This phenomenon, observed in both trained and untrained models, suggests a geometric effect explicable through percolation theory. The study employs real, interpolated, and synthetic inputs to explore input space connectivity, demonstrating its prevalence and simplicity in trained models. This research advances the understanding of neural network behavior, particularly regarding adversarial examples, and offers potential applications in adversarial detection and model interpretability. The findings provide new insights into the high-dimensional geometry of neural networks and their generalization capabilities.
The methodology employs diverse input generation techniques, including real, interpolated, and synthetic images, to comprehensively analyze input space connectivity in deep neural networks. Loss landscape analysis investigates barriers between different modes, particularly focusing on natural inputs and adversarial examples. The theoretical framework utilizes percolation theory to explain input space mode connectivity as a geometric phenomenon in high-dimensional spaces. This approach provides a foundation for understanding connectivity properties in both trained and untrained networks.
links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links links
Empirical validation on pretrained vision models demonstrates the existence of low-loss paths between different modes, supporting the theoretical claims. An adversarial detection algorithm developed from these findings highlights practical applications. The methodology extends to untrained networks, emphasizing that input space mode connectivity is a fundamental characteristic of neural architectures. Consistent use of cross-entropy loss as an evaluation metric ensures comparability across experiments. This comprehensive approach combines theoretical insights with empirical evidence to explore input space mode connectivity in deep neural networks.
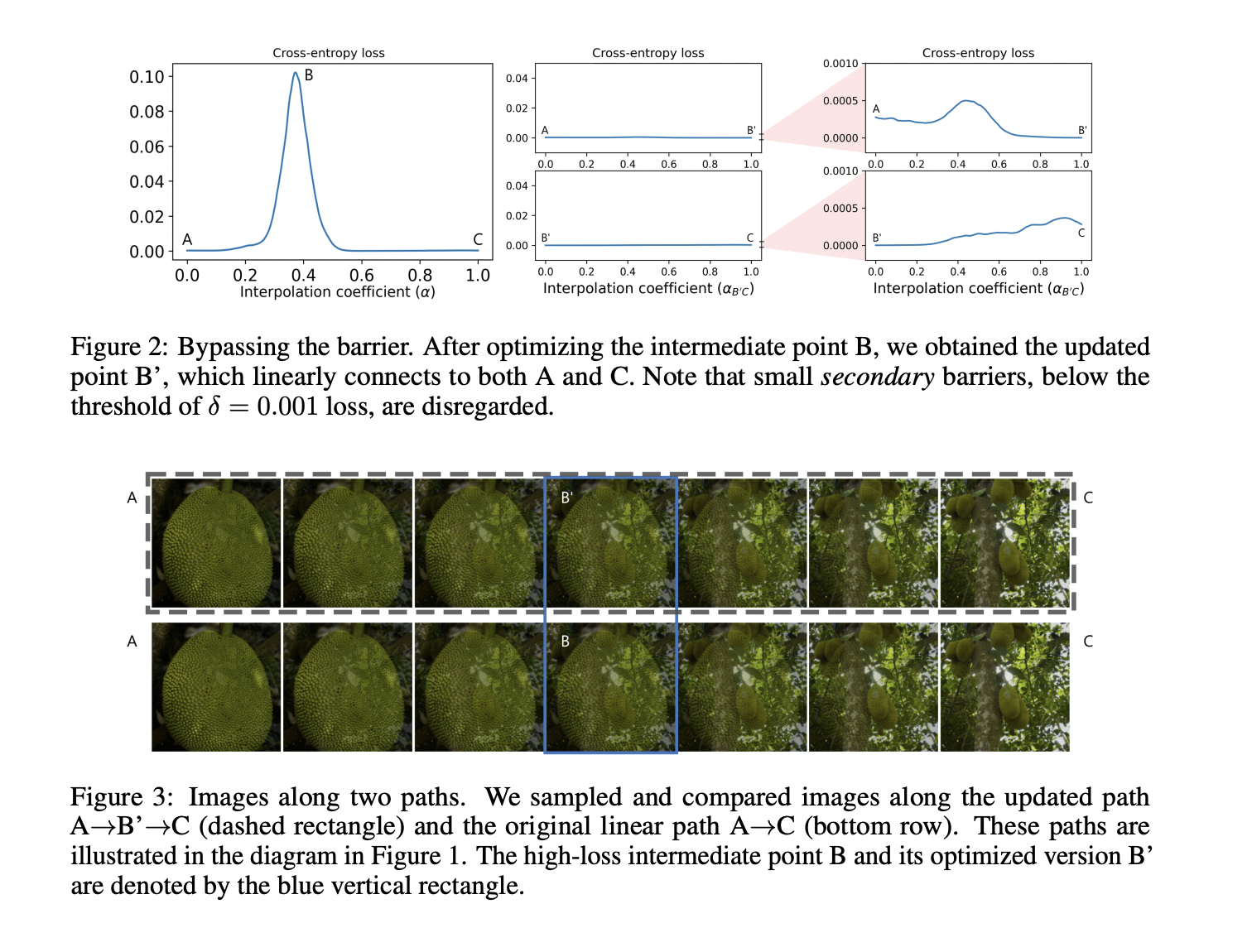
Results extend mode connectivity to the input space of deep neural networks, revealing low-loss paths between inputs, yielding similar predictions. Trained models exhibit simple, near-linear paths between connected inputs. The research distinguishes natural inputs from adversarial examples based on loss barrier heights, with real-real pairs showing low barriers and real-adversarial pairs displaying high, complex ones. This geometric phenomenon explained through percolation theory, persists in untrained models. The findings enhance understanding of model behavior, improve adversarial detection methods, and contribute to DNN interpretability.
In conclusion, the research demonstrates the existence of mode connectivity in the input space of deep networks trained for image classification. Low-loss paths consistently connect different modes, revealing a robust structure in the input space. The study differentiates natural inputs from adversarial attacks based on loss barrier heights along linear interpolant paths. This insight advances adversarial detection mechanisms and enhances deep neural network interpretability. The findings support the hypothesis that mode connectivity is an intrinsic property of high-dimensional geometry, explainable through percolation theory.
Check out the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter and join our Telegram Channel and LinkedIn Group. If you like our work, you will love our newsletter..
Don’t Forget to join our 50k+ ML SubReddit

Shoaib Nazir is a consulting intern at MarktechPost and has completed his M.Tech dual degree from the Indian Institute of Technology (IIT), Kharagpur. With a strong passion for Data Science, he is particularly interested in the diverse applications of artificial intelligence across various domains. Shoaib is driven by a desire to explore the latest technological advancements and their practical implications in everyday life. His enthusiasm for innovation and real-world problem-solving fuels his continuous learning and contribution to the field of AI